Available for CBSE, ICSE and State Board syllabus.
Call our LearnNext Expert on 1800 419 1234 (tollfree)
OR submit details below for a call back

Introducing NextGurukul app, India's Largest Collaborative Learning Community for Learners and Educators - Now available with a Fresh UI and Exciting New Features!
Install Now
CBSE X
SET - I
MATHEMATICS PAPER 2009.
Time allowed: 3 hours; Maximum Marks: 80
| General Instructions: | |
| 1) | All questions are compulsory. |
| 2) | The question paper consists of thirty questions divided into 4 sections A, B, C and D. Section A comprises of ten questions of 01 mark each, Section B comprises of five questions of 02 marks each, Section C comprises ten questions of 03 marks each and Section D comprises of five questions of 06 marks each. |
| 3) | All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question. |
| 4) | There is no overall choice. However, internal choice has been provided in one question of 02 marks each, three questions of 03 marks each and two questions of 06 marks each. You have to attempt only one of the alternatives in all such questions. |
| 5) | In question on construction, drawing should be near and exactly as per the given measurements. |
| 6) | Use of calculators is not permitted. |
Question number 1 to 10 carry 1 mark each.
1.Write whether the rational number ![]() will have a terminating
decimal expansion or a non-terminating repeating decimal
expansion.
will have a terminating
decimal expansion or a non-terminating repeating decimal
expansion.
Solution:
The rational number given in the
question is ![]() . It can also be written
as
. It can also be written
as
![]()
The above number is of type ![]() , in which x=2 and y=3.
, in which x=2 and y=3.
Since x and y are positive integers,
the rational number ![]() or
or ![]() will have a terminating
decimal expansion.
will have a terminating
decimal expansion.
2.Write the polynomial, the product and sum
of whose zeroes are ![]() and
and ![]() respectively.
respectively.
Solution:
Let us assume that ![]() and
and ![]() are the zeroes of the
polynomial.
are the zeroes of the
polynomial.
The product of the zeroes = ![]() =
= ![]()
The sum of the zeroes = ![]() =
=![]()
The required polynomial equation can be written as
![]()
= ![]()
= ![]()
If we take k=2, we will get the
polynomial as ![]() .
.
One polynomial where the product of
zeroes ![]() and sum of zeroes
and sum of zeroes ![]() , is
, is ![]()
3.
Write whether the following pair of
linear equations is consistent or not:
x + y = 14
x ? y = 4
Solution:
The equation x + y = 14 can also be written as x + y - 14 = 0
Similarly, x ? y = 4 can be written as x - y - 4 = 0
x + y -14 = 0
can be represented by ![]() where
where![]() ,
, ![]() = 1 and
= 1 and ![]() = - 14
= - 14
x + y -14 = 0 can be represented by ![]() where
where ![]() ,
, ![]() = - 1 and
= - 1 and ![]() = - 4
= - 4
![]() =
=![]()
![]() =
= ![]()
We see from above that ![]()
![]()
![]() .
.
Therefore the pair of linear equations given in the question is consistent.
4.Write the nature of roots of quadratic
equation
![]()
Solution:
The given equation can be represented
by ![]() where a=4, b=
where a=4, b=![]() and c=3.
and c=3.
The discriminant or D is given by ![]() . Substituting a=4, b=
. Substituting a=4, b=![]() and c=3 in this, we get
and c=3 in this, we get
![]() = (
= (![]() )2 - 4
)2 - 4
![]() = 48 - 48 =0.
= 48 - 48 =0.
From above, we see that there are two equal and real roots for the given quadratic equation.
5.For what value of k, are the numbers x, 2x + k and 3x + 6 three consecutive terms of an A.P.
Solution:
Let us assume that a, b and c are the three consecutive terms of the A.P. where a=x, b= 2x + k and c = 3x + 6.
For an A.P. , 2b= a + c
Substituting a=x, b= 2x + k and c = 3x + 6 in this, we get
2![]() = x + 3x + 6
= x + 3x + 6
![]() 4x + 2k = 4x + 6
4x + 2k = 4x + 6
![]() 2k = 6
2k = 6
![]() k = 3
k = 3
Thus x, 2x + k and 3x + 6 are three consecutive terms of an A.P. if k=3.
6.In a ?ABC, DE||BC. IF DE = ![]() BC and area of ?ABC =
81 cm2, find the area of ?ADE.
BC and area of ?ABC =
81 cm2, find the area of ?ADE.
Solution:
?DAE = ?BAC as it is common angle
?ADE = ?ABC since they are corresponding angles
Hence according to the AA similarity
condition, ?ADE ![]() ?ABC
?ABC
For similar triangles, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
![]()
![]() =
= ![]() =
= ![]() =
= ![]()
Since DE = ![]() BC,
BC, ![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]() =
= ![]() .
.
![]() area of ?ADE =
area of ?ADE = ![]()
![]() area of ?ABC =
area of ?ABC = ![]()
![]() 81 cm2 = 36
cm2.
81 cm2 = 36
cm2.
Hence area of ?ADE = 36 cm2.
7.If sec A = ![]() and A + B = 90°, find
the value of cosec B.
and A + B = 90°, find
the value of cosec B.
Solution:
Since A + B = 90°, A = 90° - B
![]() sec A = sec(90° - B)
sec A = sec(90° - B)
As cosec ![]() = sec(90° -
= sec(90° - ![]() ),
),
sec A = cosec B
Given: sec A = ![]()
![]() cosec
B =
cosec
B = ![]()
Hence value of cosec B is ![]() .
.
8.If the mid-point of the line segment joining the points P (6, b ? 2) and Q (?2, 4) is (2, ?3), find the value of b.
Solution:
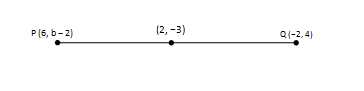
Using mid-point formula, ![]() = - 3
= - 3
![]()
![]() = - 3
= - 3
![]() b + 2 = -6
b + 2 = -6
![]() b = -8
b = -8
Hence we get the value of b as - 8.
9.The length of the minute hand of a wall clock is 7 cm. How much area does it sweep in 20 minutes?
Solution:
In 60 minutes, the angle that will be
swept by the minute hand = ![]()
![]() in 20 minutes, the angle
that will be swept by the minute hand =
in 20 minutes, the angle
that will be swept by the minute hand = ![]() 20 =
20 = ![]()
Area swept by the minute hand in 20
minutes = ![]()
![]()
![]()
![]() (7 cm)2 .
(7 cm)2 .
= ![]()
= ![]()
Hence the area swept by the minute
hand in 20 minutes is ![]()
10.
What is the lower limit of the modal
class of the following frequency distribution?
Age in (years)
0 -10
10 -20
20 - 30
30 - 40
40 - 50
50 - 60
Number of patients
16
13
6
11
27
18
Solution:
A modal class is the class interval having maximum frequency.
In the above frequency distribution, 27 is the maximum frequency and it comes in class interval 40 - 50.
Hence 40 - 50 is the modal class
![]() 40 is the lower limit of
the modal class in the given frequency distribution.
40 is the lower limit of
the modal class in the given frequency distribution.
11.
Without drawing the graph, find out
whether the lines representing the following pair of linear
equations intersect at a point, are parallel or coincident:
![]()
![]()
Solution:
If ![]() and
and ![]() are two linear
equations.
are two linear
equations.
1. If ![]() , the above equations will represent
intersecting lines
, the above equations will represent
intersecting lines
2. If ![]() , the equations will represent
coincident lines
, the equations will represent
coincident lines
3. If ![]() , the equations will represent
parallel lines
, the equations will represent
parallel lines
The equations given are :-
![]() or
or ![]()
![]() or
or ![]()
Here ![]() and
and ![]()
Similarly ![]() ,
, ![]() and
and ![]()
![]()
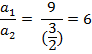
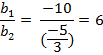 and
and
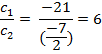
Hence ![]() , which means that the
given pair of equations represent coincident lines
, which means that the
given pair of equations represent coincident lines
12.The 17th term of an A.P. exceeds its 10th term by 7. Find the common difference.
Solution:
For an A.P. its nth term or an is an = a + (n-1) d where a is the first term and d is the common difference between the terms.
The 17th term of an A.P. or
![]()
The 10th term of the A.P or
![]()
As given in the question, the difference between 17th term and 10th term of A.P. = 7.
![]()
![]() 7d = 7
7d = 7
![]()
Hence the common difference or d between the terms of the A.P. = 1
13.
Without using trigonometric tables,
evaluate:
![]()
Solution:
![]() and
and ![]()
![]()
![]()
![]()
![]()
= ![]()
= ![]()
= 5
The value of the given expression is 5.
14.
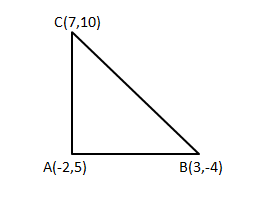
Show that the points (?2, 5); (3,
?4) and (7, 10) are the vertices of a right angled isosceles
triangle.
OR
The centre of a circle is (2? ? 1,
7) and it passes through the point (?3, ?1). If the diameter
of the circle is 20 units, then find the values(s) of ?.
Solution:
Using distance formula, we get
AB = ![]() =
= ![]() =
= ![]() =
= ![]()
BC = ![]() =
= ![]() =
= ![]() =
= ![]()
CA = ![]() =
= ![]() =
= ![]() =
= ![]()
As AB = CA, we see that the triangle is isosceles.
AB2 + CA2 = 106 + 106 =212 = BC2 .
![]() using Pythagoras
theorem, we find that the triangle is right-angled at A.
using Pythagoras
theorem, we find that the triangle is right-angled at A.
Hence we have proved that the given points (?2, 5), (3, ?4) and (7, 10) are the vertices of a right-angled triangle.
OR
The center of the circle is given as (![]() . The point it passes
through is given as (-3, -1)
. The point it passes
through is given as (-3, -1)
 |
Using distance formula, the radius of the circle or OP
= ![]()
= ![]()
= ![]()
Since the diameter of circle is given
as 20 units and diameter = ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
When ![]() , then
, then ![]()
When ![]() , then
, then ![]()
![]()
![]()
![]()
15.If C is a point lying on the line segment AB joining A (1, 1) and B (2, ?3) such that 3AC = CB, then find the coordinates of C.
Solution:
Let us assume that the coordinates of C are m and n. Point C can be represented as C(m, n).
Given: 3AC = CB
![]()
![]()
Using section formula,
![]() =
= ![]()
![]() The coordinates of point
C are (
The coordinates of point
C are (![]() )
)
16.
Show that the square of any positive
odd integer is of the form 8m + 1, for some integer m.
OR
Prove that ![]() is not a rational
number.
is not a rational
number.
Solution:
Let us represent a positive integer with 'a'
It can be represented as
![]() where
where ![]() and
and ![]() is an integer
is an integer
Hence a will be ![]()
Positive odd integer will be of the
form ![]()
Let us consider the above 4 positive odd integer forms seperately
Case 1 : ![]()
![]() is an integer
is an integer
Case 2: ![]()
![]() is an integer
is an integer
Case 3: ![]()
![]() is an integer
is an integer
Case 4: ![]()
![]() is an integer
is an integer
From all these cases we see that the
square of a positive odd integer is of the form ![]() where
where ![]() is any integer
is any integer
OR
Let us assume that ![]() is a rational number
is a rational number
If so it can be represented using
integers a and b (![]() as
as
![]()
![]()
![]()
a and b are rational numbers. So ![]() should also be rational
and
should also be rational
and ![]() should also be a
rational number. But we know that
should also be a
rational number. But we know that ![]() is an irrational number
and so our assumption is wrong.
is an irrational number
and so our assumption is wrong.
Since our assumption is false it is
proved that ![]() is not a rational
number.
is not a rational
number.
17.If the polynomial 6x4 + 8x3 ? 5x2 + ax + b is exactly divisible by the polynomial 2x2 ? 5, the find the values of a and b.
Solution:
p(x) = 6x4 + 8x3 ? 5x2 + ax + b
q(x) = 2x2 - 5
Dividing p(x) by q(x)
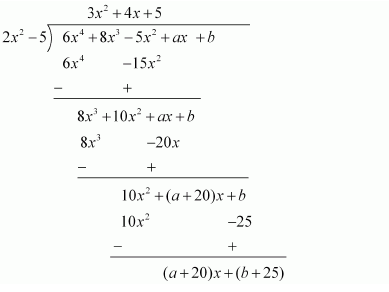
We get the remainder as ![]() .
.
As p(x) is exactly divisible by q(x), remainder should be 0.
![]() = 0
= 0
![]()
From ![]() and
and
From ![]()
Therefore the value of ![]() and
and ![]()
18.If 9th term of an A.P. is zero, prove that its 29th term is double of its 19th term.
Solution:
Let a be the 1st term and d be the common difference of the A.P.
nth term of A.P. =
![]()
![]() 9th term of
A.P =
9th term of
A.P =
![]()
Given: ![]()
![]()
![]()
![]()
19th term of A.P. =
![]()
29th term of A.P. =
![]()
![]()
Hence the 29th term of the A.P. is double the 19th term of the A.P.
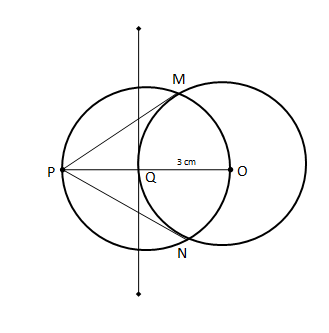
19.Draw a circle of radius 3 cm. From a point P, 6 cm away from its centre, construct a pair of tangents to the circle. Measure the lengths of the tangents.
Solution:
With radius as 3 cm, draw a circle. Mark the center point as O. Take a point P at a distance of 6 cm from O and join O and P.
Draw a perpendicular bisector to the line OP. Mark the point at which it intersects the circle as point Q.
Using Q as center and QP as radius, draw a circle. This will intersect the first circle at 2 points. Mark the points as M and N.
Join M with P to obtain line MP and N with P to obtain the line NP. MP and NP are the tangents.
On measuring, the length of the tangents, MP and NP is 5.20 cm .
20.In figure 1, two triangles ABC and DBC lie on the same side of base BC. P is a point on BC such that PQ || BA and PR || BD. Prove that QR || AD.
Solution:
Consider ![]() and
and ![]()
PQ || BA and hence according to the basic proportionality theorem, we get
![]() ---------------------
(1)
---------------------
(1)
Consider ![]() and
and ![]()
PR || BD and hence according to the basic proportionality theorem, we get
![]() -----------------------(2)
-----------------------(2)
Taking (1) and (2) together we get
![]()
![]() , from above, using
converse of proportionality theorem, we get QR|| AD.
, from above, using
converse of proportionality theorem, we get QR|| AD.
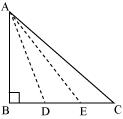
21.
In figure 2, a triangle ABC is right
angled at B. Side BC is trisected at points D and E. Prove
that 8
OR
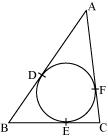
In figure 3, a circle is inscribed
in a triangle ABC having side BC = 8 cm, AC = 10 cm and AB =
12 cm. Find AD, BE and CF.
![]()
Solution:

Given: BC is trisected at D and E.
![]()
![]()
Consider ![]() . Using Pythagoras
Theorem, we get
. Using Pythagoras
Theorem, we get
![]()
![]()
![]() ---------------------(1)
---------------------(1)
Consider ![]() . Using Pythagoras
theorem, we get
. Using Pythagoras
theorem, we get
![]()
![]()
![]() -----------------------(2)
-----------------------(2)
Consider ![]() . Using Pythagoras
theorem, we get
. Using Pythagoras
theorem, we get
![]() -----------------------(3)
-----------------------(3)
We have to prove that ![]()
![]()
![]()
![]()
![]()
From (2), we know that ![]() . Hence substituting in above, we get
. Hence substituting in above, we get
![]()
Hence proved.
OR
AD and AF are tangents drawn from point A to the circle. Similarly BD and BE are tangents from point B to the circle and CE and CF are tangents from point C

The tangents drawn to the circle from any point external to the circle are equal.
![]() AD=AF
AD=AF
BD=BE and
CE =CF
Let us take AD = a, BE = b and CF = c
![]() -----(1)
-----(1)
![]() -----(2)
-----(2)
![]() ------(3)
------(3)
![]()
![]() ------(4)
------(4)
Substituting (1) in (4), we get
![]()
Substituting (2) in 4, we get
![]()
Substituting (3) in (4), we get
![]()
Thus we get
![]()
22.
Prove that
![]()
Solution:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
23.Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution:
Since the points (x, y), (1, 2) and (7, 0) are collinear, the area of the triangle formed with these three points as vertices will be zero.
Area of triangle with points (x1,y1) , (x2,y2) , (x3,y3) =
![]()
![]()
![]()
![]()
![]()
Thus the area of the triangle is ![]() . Since this area is
zero, we get
. Since this area is
zero, we get
![]()
![]() is the equation which
shows the relation between x and y if the points have to be
collinear.
is the equation which
shows the relation between x and y if the points have to be
collinear.
24.
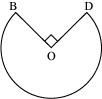
In figure 4, the shape of the top of
a table in a restaurant is that of a sector of a circle with
centre O and ?BOD
= 90°. If BO = OD = 60 cm, find
(i) the area of the top of the
table.
(ii) the perimeter of the table top.
(Take ? = 3.14)
OR
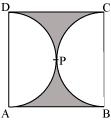
In figure 5, ABCD is a square of
side 14 cm and APD and BPC are semicircles. Find the area of
shaded region. (Take
![]() )
)
Solution:

(i) Area of table top
Area of a sector can be obtained by ![]() where
where ![]() is the angle of the
sector and r is the radius.
is the angle of the
sector and r is the radius.
Given : ![]() .
.
![]()
Hence area of table top = ![]()
![]()
![]()
![]()
![]()
Hence area of table top = ![]()
(ii) Perimeter of table top
= length of the arc BD + OB + OD
Length of the arc BD = ![]()
![]()
![]()
![]() Perimeter of the table
top =
Perimeter of the table
top = ![]()
![]()
OR

Area of the shaded region = Area of the square ABCD - (area of semicircle APD + area of semicircle BPC)
Area of square ABCD
![]() (since length of sides
of the square = 14 cm)
(since length of sides
of the square = 14 cm)
Area of semicircle APD = ![]() where r = 7 cm (AD = 14
cm,
where r = 7 cm (AD = 14
cm, ![]() )
)
![]()
Area of semicircle BPC = ![]() since r= 7 cm
since r= 7 cm
![]() Area of the shaded
region =
Area of the shaded
region = ![]()
![]()
Hence area of shaded region = ![]()
25.
A box has cards numbered 14 to 99.
Cards are mixed thoroughly and a card is drawn from the bag
at random. Find the probability that the number on the card,
drawn from the box is
(i) an odd number,
(ii) a perfect square number,
(iii) a number
divisible by 7.
Solution:
The probability of an event =
![]()
![]() Number of cards in box =
99 -14 + 1 = 86
Number of cards in box =
99 -14 + 1 = 86
(i)
Number of cards having odd number = ![]()
Hence probability of getting odd number = ![]()
(ii)
Number of cards having perfect squares
![]() ( Perfect squares between 14 and 9
are 16, 25, 36, 49, 64 and 81)
( Perfect squares between 14 and 9
are 16, 25, 36, 49, 64 and 81)
Hence probability of getting perfect square ![]()
(iii)
Number of cards with numbers divisible by 7
= 13
(Numbers divisible by 7 between 14 and 99 are 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91 and 98)
Hence probability of getting number divisible by 7
= ![]()
26.
A trader bought a number of articles
for Rs 900. Five articles were found damaged. He sold each of
the remaining articles at Rs. 2 more than what he paid for
it. He got a profit of Rs. 80 on the whole transaction. Find
the number of articles he bought.
OR
Two years ago the man's age was
three times the square of his son's age. Three years hence
his age will be four times his son's age. Find their present
ages.
Solution:
Let the total number of articles bought be 'x'
Cost of x articles = Rs 900
![]() Cost price of 1 article
=Rs
Cost price of 1 article
=Rs ![]()
Number of articles sold = x-5
Selling price of 1 article = Rs ![]()
Profit after selling x-5 articles = Rs 80
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Since number of articles will not be negative, x= 75
Hence the number of articles bought by the trader = 75
OR
Let the son's age be 'x'
Son's present age = ![]()
Son's age 2 years ago = ![]()
Man's age 2 years ago = ![]()
Man's present age = ![]()
Son's age 3 years later from present =
![]()
Man's age 3 years later from present =
![]()
Man's present age = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Since age cannot be fraction, x = 5
![]() Son's age = 5 years
Son's age = 5 years
Man's age = ![]() years
years
27.
Prove that the ratio of the areas of
two similar triangles is equal to the ratio of the squares of
their corresponding sides.
Using the above theorem prove the
following:
The area of the equilateral triangle
described on the side of a square is half the area of the
equilateral triangle described on its diagonal.
Solution:
Let the 2 similar triangles be ![]() .
.
To prove: ![]()
Let us draw AP ? BC and XQ ? YZ.

![]()
![]()
![]()
![]()
![]()
![]()
From above, we get
![]()
![]()
Using (4) and (5), we get
![]() ------------------------------------(6)
------------------------------------(6)
Substituting (6) in (3), we get
![]()
From (6), we get
![]()
To prove: ![]()
Let the sides of the square be of length 'a'
![]()
![]() (since BC is diagonal)
(since BC is diagonal)
![]()
All the angles of equilateral triangle
are ![]() and all the sides of an
equilateral triangle are equal.
and all the sides of an
equilateral triangle are equal.
Hence all equilateral triangles are similar.
![]()
![]()
Hence ![]() =
= ![]()
Therefore the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
Q28 The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
28.The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
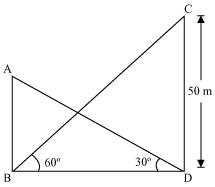
Let the building be AB and the tower CD.
Length of CD = 50 m
Consider ![]()
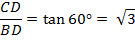
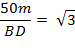
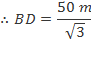
Consider ![]()
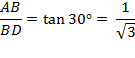
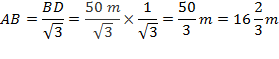
Thus the height of the building is ![]()
29.
A spherical copper shell, of
external diameter 18 cm, is melted and recast into a solid
cone of base radius 14 cm and height
OR
A bucket is in the form of a frustum
of a cone with a capacity of 12308.8 ![]() cm. Find the inner
diameter of the shell.
cm. Find the inner
diameter of the shell.
![]() . The radii of the top
and bottom circular ends of the bucket are 20 cm and 12 cm
respectively. Find the height of the bucket and also the area
of metal sheet used in making it.
. The radii of the top
and bottom circular ends of the bucket are 20 cm and 12 cm
respectively. Find the height of the bucket and also the area
of metal sheet used in making it.
Solution:
Let 'r' be the inner radius and 'R' be the external radius of the copper shell.
Given : External diameter of copper shell = 2R = 18 cm
![]()
Volume of the spherical copper shell =
![]()
![]()
The spherical copper shell is made into a solid cone
Hence volume of solid cone = volume of spherical shell
Volume of cone = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence ![]()
Therefore inner radius of the spherical copper shell = 8 cm and hence inner diameter = 16 cm
OR
Let the top radius of the bucket be 'r' and bottom radius of bucket be 'R'
r = 20 cm and R = 12 cm
Let the height of the bucket be 'h'
Volume of the bucket = ![]()
![]()
![]()
![]()
![]()
Let 's' be the slant height of the metal sheet
![]()
![]() =
= ![]() =
= ![]() = 17 cm
= 17 cm
The area of the metal sheet used in making the bucket
= CSA of the bucket + area of the bottom circular end of the bucket
= ![]()
![]()
![]()
![]()
![]()
![]()
30.
Find the mode, median and mean for
the following data:
Marks obtained
25 ? 35
35 ? 45
45 ? 55
55 ? 65
65 ? 75
75 ? 85
Number of students
7
31
33
17
11
1
Solution:
(a). Mode
|
Marks obtained |
25?35 |
35?45 |
45?55 |
55?65 |
65?75 |
75?85 |
|
Number of students |
7 |
31 |
33 |
17 |
11 |
1 |
The maximum frequency is 33 and the class having the maximum frequency is 45?55.
![]() modal class = 45?55.
modal class = 45?55.
Lower class limit (l) of modal class = 45
Frequency (f1) of modal class = 33
Frequency (f0) of class preceding the modal class = 31
Frequency (f2) of class succeeding the modal class = 17
Class size (h) = 10
![]()
![]()
![]()
![]()
![]() = 46.11(approximate)
= 46.11(approximate)
(B). Median
Let us calculate the cumulate frequency of the data in another column:-
|
Marks obtained |
Number of students |
Cumulative frequency |
|
25 ? 35 |
7 |
7 |
|
35 ? 45 |
31 |
38 |
|
45 ? 55 |
33 |
71 |
|
55 ? 65 |
17 |
88 |
|
65 ? 75 |
11 |
99 |
|
75 ? 85 |
1 |
100 |
We obtain n as 100
![]()
Cumulative frequency (cf) just greater than 50 = 71
71 comes under in the class interval 45-55. Hence median class = 45-55
Lower limit (l) of median class = 45
Class size (h) = 10
Frequency (f) of median class = 33
Cumulative frequency (cf) of class preceding median class = 38
Median = ![]()
![]()
(C). Mean
The class marks for each interval can be calculated by using the formula
![]()
Taking 60 as assured mean (a), di, ui, and fiui can be calculated as follows:
|
Marks obtained |
Number of students (fi) |
xi |
di = xi ? 60 |
|
fiui |
|
25?35 |
7 |
30 |
? 30 |
? 3 |
? 21 |
|
35?45 |
31 |
40 |
? 20 |
? 2 |
? 62 |
|
45?55 |
33 |
50 |
? 10 |
? 1 |
? 33 |
|
55?65 |
17 |
60 |
0 |
0 |
0 |
|
65?75 |
11 |
70 |
10 |
1 |
11 |
|
75?85 |
1 |
80 |
20 |
2 |
2 |
|
Total |
100 |
? 103 |
Mean = ![]()
![]()
![]() mode = 46.11, median =
48.63 and mean = 49.7
mode = 46.11, median =
48.63 and mean = 49.7
| Section A | Section B | Section C | Section D |